Change in productivity: Solution

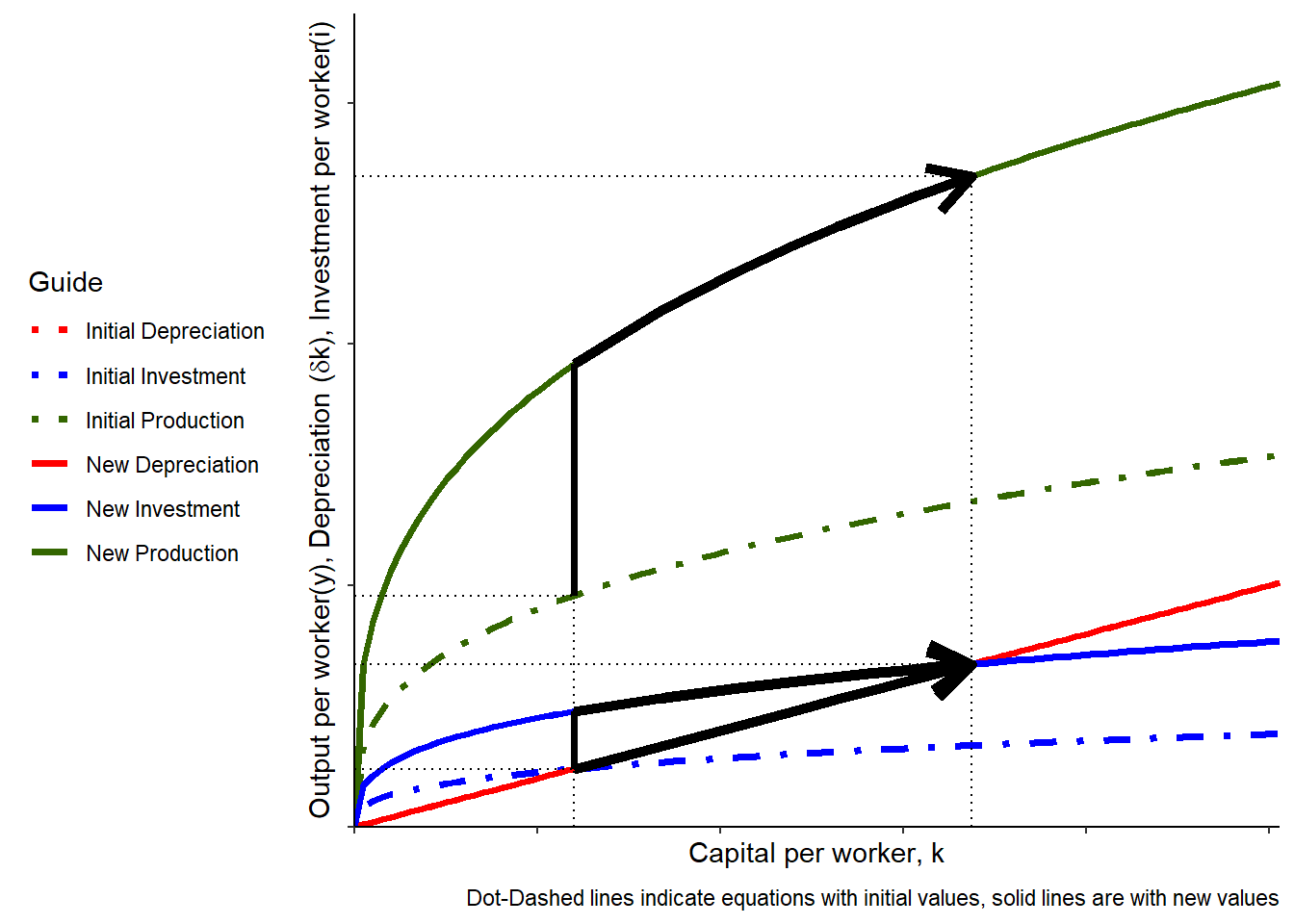
The increase in productivity means that at every level of capital per worker, workers produce more output. This also means that at a given rate of saving, more is invested. So there is an initial increase in output and investment due to the change in productivity. Then, because investment is greater than depreciation, capital per worker begins to grow over time, which leads to further increases in output, investment and depreciation. This continues until the economy reaches its new steady state with a higher level of capital per worker. Note that consumption is a constant fraction of output per worker, and the savings rate hasn’t changed, so consumption increases over time as well.

Unlike changes in savings rates, there is no tradeoff between current and future consumption when productivity increases.

This observation is quite important. We assumed that productivity was constant. This means that in steady state, GDP per worker doesn’t change; all of the growth in the model is simply transitioning from one steady state to another. This is at odds with the fact that most rich countries seem to grow at a similar, positive rate. However, the ``full-blown’’ Solow model (presented in the Appendix C ) actually assumes that productivity grows at a constant rate over time. In the long run, this growth rate of productivity is the same as the growth rate of GDP per worker. We could understand this growth rate as the rate at which technology or efficiency is increasing at the “frontier,” and perhaps is related to the productivity of research scientists. Trying to explain the growth rate of productivity endogenously - within the model - is what earned Paul Romer the 2018 Economics Nobel Prize.

5.3 Numerical and graphical dynamics

Below, I’ve embedded an application that lets you select “start” and “end” parameters, calculate steady state values, and plots the comparative graphs, including the path that the economy follows to get there. This may be helpful for checking your work as you practive using the model. It’s also linked here: Solow dynamics app