Frequency refers to how high or how low the note sounds (pitch). The term pitch is used to describe frequencies within the range of human hearing.
Amplitude refers to how loud or soft the sound is.
Duration refers to how long a sound lasts.
Timbre ( pronounced TAM-burr) refers to the characteristic sound or tone color of an instrument. A violin has a different timbre than a piano.
Envelope refers to the shape or contour of the sound as it evolves over time. A simple envelope consists of three parts: attack, sustain, and decay. An acoustic guitar has a sharp attack, little sustain and a rapid decay. A piano has a sharp attack, medium sustain, and medium decay. Voice, wind, and string instruments can shape the individual attack, sustain, and decay portions of the sound.
Location describes the sound placement relative to our listening position. Sound is perceived in three dimensional space based on the time difference it reaches our left and right eardrums.
These six properties of sound are studied in the fields of music, physics, acoustics, digital signal processing (DSP), computer science, electrical engineering, psychology, and biology. This course will study these properties from the perspective of music, MIDI, and digital audio.
MIDI (Musical Instrument Digital Interface) is a hardware and software specification that enables computers and synthesizers to communicate through digital electronics . The first version of the MIDI standard was published in 1983. MIDI itself does not produce any sounds, it simply tells a synthesizer to turn notes on and off. The quality of the sounds you hear are dependent on the sounds built into the synthesizer. Cheap MIDI synthesizers sound like toys. Expensive MIDI synthesizers can realistically reproduce a full orchestra, however they may cost over $10,000. The MIDI Manufacturers Association (www.midi.org) is in charge of all things MIDI.
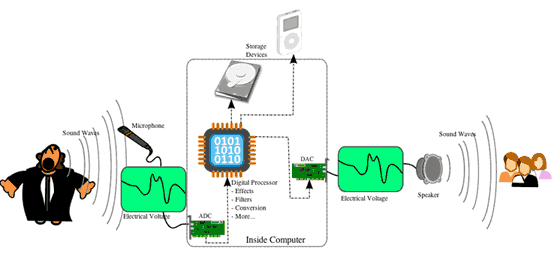
Digital audio is a mix of mathematics, computer science, and physics. Sound waves we hear are represented as a stream of numbers. An Analog Digital Converter (ADC) converts an analog signal (e.g., voltage fluctuations from a microphone) into numbers that are sent to a computer. The computer processes the numbers and sends them on to a Digital Analog Converter (DAC). The DAC converts the numbers back into an analog signal that drives a speaker.

http://upload.wikimedia.org/wikipedia/commons/8/84/A-D-A_Flow.svg
An analog signal is a continuous signal. A digital signal is a discrete signal. Analog signal values are known for all moments in time. Digital signals are only known at certain specified times.
| Continuous Analog Signal | Discrete Digital Signal |
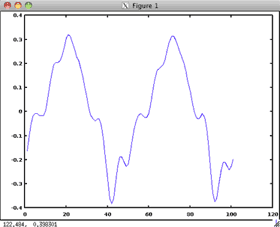 |
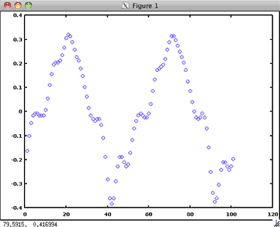 |
These screen shots were captured using the open source, cross platform software Octave. (http://octave.sourceforge.net/)
These prefixes refer to numerical quantities. For example a 1 gigahertz computer's CPU is timed with a clock running in nanoseconds. Or, a slow digital audio recorder can record 23 samples every microsecond. I purchased my first computer hard drive in 1987, it was a 1 megabyte drive and cost $1000. I recently purchased a 3 terabyte hard drive for $200.
Prefix |
Value |
Abbreviation |
| Tera | 1,000,000,000,000 | T |
| Giga | 1,000,000,000 | G |
| Mega | 1,000,000 | M |
| Kilo | 1,000 | K |
| Milli | 0.001 | m |
| Micro | .000001 | μ |
| Nano | .000000001 | n |
| Pico | .000000000001 | p |
Frequency is measured in Hertz (Hz). One Hz is one cycle per second. Human hearing lies within the range of 20Hz - 20,000Hz. As we get older the upper range of our hearing diminishes. Human speech generally falls in the range from 85 Hz - 1100 Hz. Two frequencies are an octave apart if one of them is exactly twice the frequency of the other. These frequencies are each one octave higher than the one before: 100Hz, 200Hz, 400Hz, 800Hz, and 1600Hz.
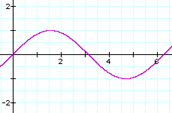
Frequency and pitch are often thought to be synonymous. However, there is a subtle distinction between them. A pure sine wave is the only sound that consists of one and only one frequency. Most musical sounds we hear contain a mix of several harmonically related frequencies. Nonetheless, musical frequencies are referred to as pitch and are given a names like "Middle C" or "the A above Middle C".
The frequency spectrum used in music is a discrete system, where only a select number of specific frequencies are used. For example, the piano uses 88 of them from 27.5 Hz to
4186 Hz. The modern system of tuning is called Equal Temperament and divides the octave 12 equal parts. The frequency ratio between any two neighboring notes is ![]() .
.
Lowest A
|
A 440
|
Highest C
|
The higher the frequency, the higher the pitch. The lower the frequency, the lower the pitch. High pitches are written higher on the musical staff than low pitches. High notes on the piano are on the right, and low notes are on the left as you're facing the piano.
Low frequency = low pitch |
High frequency = high pitch |
 |
 |
MIDI represents frequency as a MIDI note number corresponding to notes on the piano. The 88 keys on the piano are assigned MIDI note numbers 21-108, with middle C as note number 60. You can move up or down an octave in MIDI by adding or subtracting 12 from the MIDI note number. MIDI is capable of altering the frequency of a note using using the "pitch bend" command. A MIDI Tuning Extension permits microtonal tuning for each of the 128 MIDI note numbers. However, not all synthesizers support micro tuning.
Physics and digital signal processing (DSP) deal with very large frequency ranges. The audio spectrum is a very small part of that range, a relatively narrow band between 20 - 20,000 Hz. The Audio band spans 20000 (![]() ) Hz out of a total bandwidth of
) Hz out of a total bandwidth of ![]() Hz. Because of the extreme differences between audio waves and gamma waves, a logarithmic scale was used for the graph.
Hz. Because of the extreme differences between audio waves and gamma waves, a logarithmic scale was used for the graph.
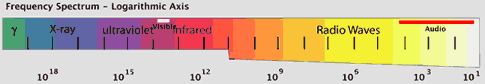
https://upload.wikimedia.org/wikipedia/commons/7/72/Radio_transmition_diagram_en.png, modified JE
The "purest" pitched tone is a sine wave. The formula for a sampled sine wave is shown below where n is a positive integer sample number, f is the frequency in Hz, SR is the sampling rate in samples per second, and θ is the phase in radians.
![]()
Many complex tones can be generated by adding, subtracting, and multiplying sine waves.
Any frequency is possible and any tuning system is possible. You could divide the octave into N parts with a frequency spacing of ![]() between notes instead of the twelve equally spaced half steps used in Equal Temperament.
between notes instead of the twelve equally spaced half steps used in Equal Temperament.
The amplitude of a sound is a measure of it's power and is measured in decibels. We perceive amplitude as loud and soft. Studies in hearing show that we perceive sounds at very low and very high frequencies as being softer than sounds in the middle frequencies, even though they have the same amplitude.
The musical term for amplitude is dynamics. There are nine common music notation symbols used used to represent dynamics. From extremely loud to silence they are:
Symbol |
Name |
Performed |
fortississimo |
as loud as possible |
|
fortissimo |
very loud |
|
forte |
loud |
|
mezzo forte |
medium loud |
|
mezzo piano |
medium soft |
|
piano |
soft |
|
pianissimo |
very soft |
|
pianississimo |
as soft as possible |
|
rest |
silence |
The pianoforte is the ancestor of the modern piano and was invented in Italy around 1710 by Bartolomeo Cristofori. It was the first keyboard instrument that could play soft (piano) or loud (forte) depending on the force applied to the keys, thus its name. If it had been invented in England we might know it as the softloud.
The MIDI term for amplitude is velocity. MIDI velocity numbers range from 0-127. Higher velocities are louder.
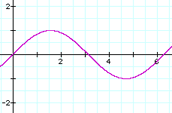
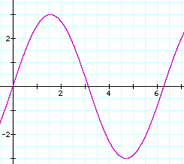
The amplitude of a sound wave determines its relative loudness. Looking at a graph of a sound wave, the amplitude is the height of the wave. These two sound waves have the same frequency but differ in amplitude. The one with the higher amplitude sounds the loudest.
Low amplitude = soft sound |
High amplitude = loud sound |
 |
 |
Amplitude is measured in decibels. Decibels have no physical units, they are pure numbers that express a ratio of how much louder or softer one sound is to another. Because our ears are so sensitive to a huge range of sound, decibels use a logarithmic rather than a linear scale according to this formula.
![]()
Positive dB's represent an increase in volume (gain) and negative dB's represent a decrease (attenuation) in volume. Doubling the amplitude results in a 6 dB gain and the sound seems twice as loud. Halving the amplitude results in a 6 dB attenuation, or a -6 dB gain, and the sound seems half as loud. When the amplitude is changed by a factor of ten the decibel change is 20 dB. Every 10 decibel change
represents a power of ten increase in sound intensity. For example, the intensity difference between the softest
symphonic music (20 dB) and loudest symphonic music (100 db) differs by a
factor of 100,000,000 (10 to the 8th power). This table shows some relative
decibel levels. Read 10^3 as ![]() .
.
Decibels Logarithmic Scale |
Magnitude Linear Scale |
Description
|
160 |
10^16 |
|
150 |
10^15 |
|
140 |
10^14 |
Jet takeoff |
130 |
10^13 |
|
120 |
10^12 |
Threshold of pain |
110 |
10^11 |
|
100 |
10^10 |
Loudest symphonic music |
90 |
10^9 |
|
80 |
10^8 |
Vacuum Cleaner |
70 |
10^7 |
|
60 |
10^6 |
Conversation |
50 |
10^5 |
|
40 |
10^4 |
|
30 |
10^3 |
|
20 |
10^2 |
Whispering |
10 |
10^1 |
|
1 |
10^0 |
Threshold of hearing |
0 |
Silence |
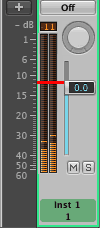
Digital audio often reverses the decibel scale making 0 dB the loudest sound that can be accurately produced by the hardware without distortion. Softer sounds are measured as negative decibels below zero. Software decibel scales often use a portion of the 0 dB to 120 dB range and may choose an arbitrary value for the 0 dB point. This dB scale is found in the Logic Pro software. The dB scale on the left goes from 0 dB down to -60 dB. The 0.0 dB setting on the volume fader on the right corresponds to -11 dB on the dB scale.
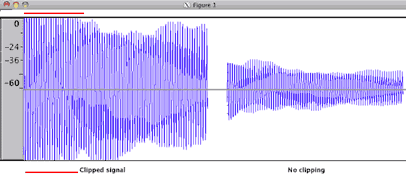
When recording digital audio, you never want the sound to stay under well under 0 dB. Notice the flat tops on the signal on the left at the 0 dB mark. That's referred to as digital clipping and it sounds terrible. The screen shots were captured using the open source cross platform software Audacity that you'll be using later in the course. (http://audacity.sourceforge.net/)
 |
|
When we talk about duration we're talking about time. We need to know two events related to the time of a sound, when did it start and how long did it last. In music and digital audio, time usually starts at zero. How time is tracked is usually a variation on chronological time or proportional time. Here are some examples.
"When I heard the first sound, I looked at my digital watch and it was 4:25:13. When I heard the second sound it was 4:25:17. The first sound had already stopped by then."
We know the starting time of both sounds but we don't know when the first sound stopped.
"When I heard the first sound, I started the digital timer on my watch. The sound ended exactly 1.52 seconds later. I heard the second sound a little later but wasn't able to reset the timer."
We know the duration of the first sound but we don't know the exact time either the first or second sound started.
"I just happened to be taking my pulse when I heard the first sound. I was on pulse count 8. Because I was also looking at my watch, I also noticed the time was 4:25:13. I kept counting my pulse and the sound stopped after four counts. I heard the second sound start four counts later. I had just been running and my pulse rate was a fast 120 beats a minute."
We know the first sound started at time 4:25:13 and lasted for 4 pulses or 2 seconds. We know that the second sound started 2 seconds after that.
The proportional time example is very similar to the way time is kept in music. A metronome supplies a steady source of beats separated by equal units of time. One musical note value (often a quarter note) is chosen as the beat unit that corresponds to one click of the metronome. All other note values are a proportional to that. Metronome clicks can come at a slow, medium, or fast pace. The speed of the metronome clicks is measured in beats per minute and is called the tempo. Whether the tempo is slow or fast, the rhythmic proportions between the notes remains the same. The actual duration of each note expands or contracts in proportion to the tempo.
Time is not defined in the MIDI standard. The software uses the computer clock to keep track of time, often in milliseconds, sometimes in microseconds. Here's a recipe (pseudo code) to play two quarter notes at a tempo of 60.
Duration in digital audio is a function of the sampling rate. Audio CD's are sampled at a rate of 44,100 samples per second with a bit depth of 16. Bit depth refers to the range of amplitude values. The largest number that can be expressed in sixteen bits is ![]() or 65,536. To put audio sampling in perspective, let's graph of one second of sound at the CD sampling rate and bit depth. Start with a very large piece of paper and draw tick marks along X axis, placing each tick exactly one millimeter apart. You'll need 44,100 tick marks which will extend about 44.1 meters (145 feet). Next you need place tick marks spaced one millimeter apart on the Y axis to represent the 16 bit amplitude values. Let's put half the ticks above the X axis and half below. You'll need 32.768 meters (about 107 feet) above and below the X axis. Now draw a squiggly wave shape above and below the X axis, from the origin to the end of the 44100th sample while staying within the Y axis boundaries. Next carefully measure the waveform height in millimeters above or below the X axis at every millimeter sample point point along the 145 foot X axis. Write these numbers down in a single file column. You've just sampled one second of a sound wave at the CD audio rate. It probably took longer than one second; definitely not real time sampling.
or 65,536. To put audio sampling in perspective, let's graph of one second of sound at the CD sampling rate and bit depth. Start with a very large piece of paper and draw tick marks along X axis, placing each tick exactly one millimeter apart. You'll need 44,100 tick marks which will extend about 44.1 meters (145 feet). Next you need place tick marks spaced one millimeter apart on the Y axis to represent the 16 bit amplitude values. Let's put half the ticks above the X axis and half below. You'll need 32.768 meters (about 107 feet) above and below the X axis. Now draw a squiggly wave shape above and below the X axis, from the origin to the end of the 44100th sample while staying within the Y axis boundaries. Next carefully measure the waveform height in millimeters above or below the X axis at every millimeter sample point point along the 145 foot X axis. Write these numbers down in a single file column. You've just sampled one second of a sound wave at the CD audio rate. It probably took longer than one second; definitely not real time sampling.
Digital sampling is done with specialized hardware called an Analog to Digital Converter (ADC). The ADC electronics contain a clock running at 44100 Hz. At every tick of the clock, the ADC reads the value of an electrical voltage at its input which is often a microphone. That voltage is stored as a 16 bit number. Bit depths of 24 are also used in today's audio equipment. A bit depth of 24 can use 16,777,216 different values to represent the amplitude.
The counterpart to the ADC is the DAC (Digital to Analog Converter) that converts the sample numbers back into an analog signal that can be played through a speaker. Most modern computers have consumer quality ADC and DAC converters built in. Professional recording studios use external hardware ADC's and DAC's that often cost thousands of or tens of thousands of dollars.
Timbre (pronounced TAM-burr) refers to the tone color of a sound. It's what makes a piano sound different from a flute or violin. The timbre of a musical instrument is determined by its physical construction and shape. Sounds with different timbres have different wave shapes. Here are the waveforms of several different instruments playing the pitch A440.
Piano |
|
|
Violin |
||
Flute |
||
Oboe |
||
Trumpet |
||
Electric Guitar |
||
Bell |
||
Snare Drum |
Timbre in music is specified as text in the score, like Sonata for flute, oboe and piano. Timbre changes may be specified in the score as special effects like growls, harmonics, slaps, scrapes, or by attaching mutes to the instrument.
Timbre in MIDI is changed by pushing hardware buttons or sending a MIDI message called the Patch change command.
Different timbres have different squiggly waveform shapes. More precisely, timbre is defined by the relative strength of the individual components present in the frequency spectrum of the sound as it evolves over time.The method of obtaining a frequency spectrum is based on the mathematics of the Fourier transform. The Fourier theorem states that any periodic waveform can be reproduced as a sum of a series of sine waves at integer multiples of a fundamental frequency with well chosen amplitudes and phases.

The pure mathematics sum would have an infinite number of terms. However, in digital audio a reasonable number works quite well.
The Fast Fourier Transform (FFT) is arguably the single most important tool in the field of digital signal processing. It can convert a sampled waveform from the time domain waveform into the frequency domain and back again. By adjusting and manipulating individual components in the frequency domain it is possible to track pitch changes; create brand new sounds; create filters that modify the sound; morph one sound into another; stretch the time without changing the pitch; and change the pitch without affecting the time. Within the last 10 years, desktop computers have become fast enough to process these DSP effects in real time.
Here are three spectrum views of a violin playing the note A440. The standard FFT displays the frequency spectrum. You can see three prominent peaks near 440 Hz, 880 Hz, and 1320 Hz. Those are the first three notes of the harmonic series, f, 2f, and 3f, when f equals 440 Hz. The sonogram displays the same data plotted with time on the X axis and frequency on the Y axis. The spectrogram displays the same data with the axes reversed from the sonogram.
| Standard FFT | 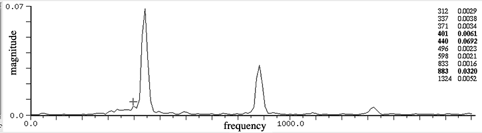 |
| Sonogram | 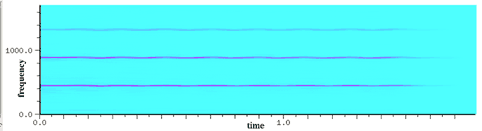 |
| Spectrogram | 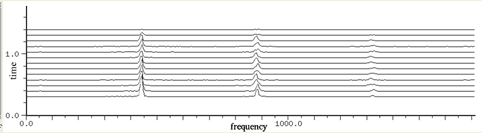 |
These screen shots were captured in the open source, cross platform sound editor Snd. (https://ccrma.stanford.edu/software/snd/)
The term envelope is used to describe the shape of a sound over the life of the note. Does it start abruptly or gradually? Does it sustain uniformly? Does it die away quickly or slowly?
The performers touch or breath can shape the envelope of a musical sound. Another term for this is articulation
A sound envelope in MIDI may be built in to the sound itself or it may be controlled through an Attack, Decay, Sustain, Release (ADSR) envelope. ADSR envelopes can sometimes be adjusted by tweaking knobs and buttons on the hardware or in the software. An ADSR envelope can be simulated in MIDI with volume or expression control messages.
The envelope of a sound is the outline of the waveform's amplitude changing over time as seen on an oscilloscope or in sound editing software.
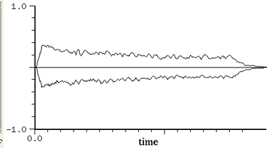
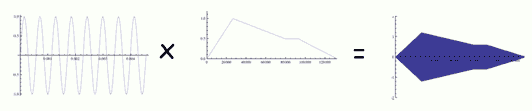
You can mathematically "envelope" a waveform by creating a second wave (amplitude values 0-1) that represents the envelope. The second wave must be the same duration as the first wave. When you multiply the samples of the original wave by the envelope wave, you create a third waveform conformed to the shape of the envelope.
Many sound editing software programs have functions to create sound envelopes. This example was created in Audacity.
 |
This second example was created in SoundTrack Pro, a part of Logic Studio.
Location refers to the listener's perception of where the sound originated.
The location of the sound is usually not specified in the score but is determined by the standing or seating arrangement of the performers.
MIDI restricts the location of sound to the two dimensional left right stereo field. The MIDI Pan control message can be used to position the sound from far left to far right or anywhere in between. If the sound is centered, equal volumes appear in the left and right speaker. If more signal is sent to the left speaker than to the right speaker, the sound will be heard coming from the left.
Sophisticated mathematical formulas can create a three dimensional sound from two dimensional stereo headphones or speakers. Waveforms can be played with multiple delayed versions of themselves to simulate the reverberation characteristics of an acoustic space.
You can calculate the distance between crests of a sound wave if you know its frequency. The speed of sound equals 791 mph or 1160.1 feet/second
(sea level, 59 degrees F). In one second the note A440 goes through 440 cycles
and has traveled 1160 feet. Therefore the distance between crests from one cycle
to the next is 2.64 feet (1160.1 ft/sec ÷ 440 cycle/sec = 2.64 feet/cycle). The distance between crests for the lowest note on the piano (27.5 Hz) is 42
feet and 3.3 inches for the highest note (4186 Hz).
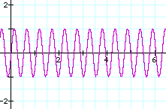
When two notes are slightly out of tune they produce beats. In this example, the first sound is a sine wave at 440 Hz, the second is 441 Hz, and the third is the combination of the two. When combined, their waveforms create audible interference patterns called beats. It's very difficult to hear the difference between the 440 Hz and 441 Hz sounds when played individually, but when they're combined it's easy to hear the beats. The rate of beating is equal to the difference in frequencies. In this example the beating rate is 1 Hz.
Sine wave at 440 Hz |
|
Sine wave at 441 Hz |
|
440 Hz and 441 Hz combined |
The definition of being "in tune" is the absence of beats. As the two notes get further out of tune, the beats become faster. As the two notes get closer to being in tune, the beats become slower. When there are no perceptible beats, the two notes are in tune.
The strings of this piano note are slightly out of tune. Listen for beats as the sound decays.
Posted in Physics, 21st November 2011 13:00 GMT
US researchers recently named the atomic clock at the UK's National Physical Laboratory (NPL) in London the most accurate atomic timepiece on the planet. Experts from the University of Pennsylvania found that NPL-CSF2 loses just one nanosecond every two months.
http://www.theregister.co.uk/2011/11/21/npl_measuring_the_second/
At that rate the clock will be one second off in just over 166 million years.
Revised John Ellinger, January - September 2013