Harmonic Interval
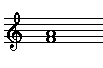
Ascending
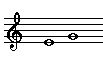
Descending
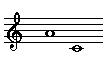
When you play two notes either simultaneously or in succession, you're playing an interval. Intervals are classified according to their size and their quality. Size is the measure of how far apart the two notes are. Quality is an adjective that further describes the size. For example, a half step is called a minor second and a whole step is called a major second. The size is a second. The quality is major or minor.
Intervals can appear in harmonic or melodic form. In harmonic form, the two notes are played simultaneously. In melodic form, the two notes notes are played in succession. Melodic intervals can be either ascending or descending.
Harmonic Interval |
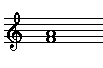 |
|
Melodic Interval Ascending |
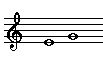 |
|
Melodic Interval Descending |
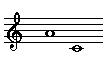 |
Size is determined by counting the number of lines and spaces (or alphabet letters) spanning the two notes, including the beginning and end. For example, the size of the interval from C up to E is a third (CDE spans three letters, or three lines and spaces), D up to A is a fifth (DEFGA spans five lines and spaces), and E up to C is a sixth (EFGABC spans six alphabet letters), etc.
| Size |
Notation |
Number of Lines and Spaces or Alphabet Letters Apart Counting Both the Beginning and End. |
|
| Unison |
|
1 |
|
| Second |
|
2 |
|
| Third |
|
3 |
|
| Fourth |
|
4 |
|
| Fifth |
|
5 |
|
| Sixth |
|
6 |
|
| Seventh |
|
7 |
|
| Octave |
|
8 |
|
| Ninth |
|
9 |
|
| Tenth |
|
10 |
Question
What is the size of the interval from C to E?
Answer
It depends on whether it's an ascending interval or a descending interval. The interval C up to E is a third, but the interval C down to E is a sixth.
| Notes |
Notation |
Size |
| C
up to E |
|
Third |
| C
down to E |
|
Sixth |
When calculating interval sizes, accidentals are ignored. The intervals C-E and C-Eb are both thirds. They sound different because they contain a different number of half steps. The third from C-E contains four half steps. The third from C-Eb contains three half steps. The larger third is called the major third, the smaller third is called the minor third.
Name |
Half Steps |
Notation |
Sound |
Minor Third |
3 |
||
Major Third |
4 |
Quality is used to distinguish intervals of the same size but with different numbers of half steps. The terms used for quality are:
Intervals are classified as perfect or imperfect. Unisons, fourths, fifths, and octaves are termed perfect intervals. Seconds, thirds, sixths, and sevenths are termed imperfect intervals.
| Class | Intervals |
| Perfect | Unison, Fourth, Fifth, Octave |
| Imperfect | Seconds, Thirds, Sixths, Sevenths |
Perfect intervals are the unison, fourth, fifth, and octave. They occur naturally in the major scale between scale note 1 and scale notes 1, 4, 5, and 8.
| Name |
Notation
in G Major |
Notes in G Major Scale |
| Perfect
Unison |
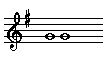 |
1 - 1 |
| Perfect
Fourth |
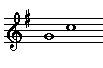 |
1 - 4 |
| Perfect
Fifth |
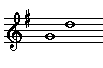 |
1 - 5 |
| Perfect
Octave |
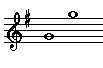 |
1 - 8 |
Imperfect intervals are the seconds, thirds, sixths, and sevenths. They come in two forms, Major and Minor.
Major Intervals
Major seconds, thirds, sixths, and sevenths occur naturally in the ascending major scale between scale note 1 and scale notes 2, 3, 6, and 7.
| Name |
Notation
in F Major |
Scale
Notes in F Major |
| Major
Second |
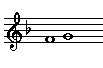 |
1
- 2 |
| Major
Third |
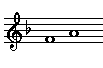 |
1
- 3 |
| Major
Sixth |
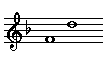 |
1
- 6 |
| Major
Seventh |
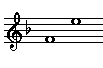 |
1
- 7 |
Minor Intervals
Minor seconds, thirds, sixths, and sevenths occur naturally in the descending major scale between scale note 8 and scale notes 7, 6, 3, and 2.
| Name |
Notation
in F Major |
Scale
Notes in F Major |
| Minor
Second |
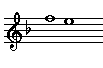 |
8
- 7 |
| Minor
Third |
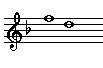 |
8
- 6 |
| Minor
Sixth |
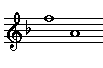 |
8
- 3 |
| Minor
Seventh |
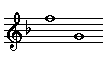 |
8
- 2 |
Perfect intervals are never major or minor. Likewise, major and minor intervals are never perfect.
Intervals can also be classified as Consonant and Dissonant.
| Perfect |
Major |
Minor |
|
| Consonant | P1,
P4, P5, P8 |
m3, M3, M6 |
m3, m6 |
| Dissonant | M2,
M7 |
m2,
m7 |
If you expand or contract an interval by a half step you change its quality. The size may stay the same. The resulting quality depends on whether you alter a perfect interval or an imperfect (major or minor) interval.
Altered Perfect
When you alter a perfect interval by a half step it becomes either diminished or augmented. When a perfect interval is made one half step larger it becomes augmented. When a perfect interval is made one half step smaller it becomes diminished.
![]()
You can expand or contract the interval from either the top or bottom note.
Altered Imperfect
When you alter an imperfect interval by a half step it becomes either diminished, minor, major, or augmented as shown in the following diagram.
![]()
When a major interval is made one half step larger it becomes augmented. When a major interval is made one half step smaller it becomes minor. When a minor interval is made one half step larger it becomes major. When a minor interval is made one half step smaller it becomes diminished.
Altered Diminished / Augmented
An augmented interval made one half step larger becomes doubly augmented. A diminished interval made one half step smaller becomes doubly diminished.
A tritone gets its name because it contains three whole steps WWW. The intervals of a diminished fifth and an augmented fourth are both tritones because they both contain six half steps.
![]() B - F = WWW and F - B = WWW
B - F = WWW and F - B = WWW
A common naming convention for intervals uses a combination of numbers and lower and upper case letters.
Perfect, Major, Augmented
minor, diminished
numbers 1 to 13
P, M, m, d, and A (note case)
P1, m2, M2, d3, m3, M3, A3, P4, A4, d5, P5, m6, M6, m7, M7, P8
To fully identify an interval you need to know both its quality and size.
There are two methods you can use to identify intervals, the easy way and the hard way. If you know your Major scales, the easy way is really easy.
In a major scale all ascending intervals are either perfect or major when compared with the first note of the scale.
Step 1. Construct the major scale that begins on the lower note of the interval.
Step 2. Determine if the upper note of the interval occurs naturally in that major scale. If it does, then unisons, 4ths, 5ths and 8ves are perfect, and 2nds, 3rds, 6ths, and 7ths are major.

Step 3. If the upper note of the interval does not belong to that major scale, determine how it differs from the interval of the same size that does occur in the major scale. Based on the half step difference from major scale interval, determine the quality according to this diagram.
1. Find the interval size by counting the lines and spaces between the two notes (including both notes).
2. Count the half steps contained in the interval, then use the table of intervals and then use the table of interval sizes to determine the quality.
Note: The Table of Intervals shown below lists only the most common names for an interval. Intervals that have the same number of half steps can have different names. For example an augmented fourth and a diminished fifth both have six half steps.
| Half Steps |
Label |
Name |
Notation |
Sound |
| 0 |
PU |
Perfect Unison | ||
| 1 |
m2 |
Minor Second | ||
| 2 |
M2 |
Major Second | ||
| 3 |
m3 |
Minor Third | ||
| 4 |
M3 |
Major Third | ||
| 5 |
P4 |
Perfect Fourth | ||
| 6 |
A4,
d5 |
Augmented Fourth, |
||
| 7 |
P5 |
Perfect Fifth | ||
| 8 |
m6 |
Minor Sixth | ||
| 9 |
M6 |
Major Sixth | ||
| 10 |
m7 |
Minor Seventh | ||
| 11 |
M7 |
Major Seventh | ||
| 12 |
P8 |
Perfect Octave | ||
| 13 |
m9 |
Minor Ninth | ||
| 14 |
M9 |
Major Ninth | ||
| 15 |
m10 |
Minor Tenth | ||
| 16 |
M10 |
Major Tenth |
Intervals that sound the same (contain the same number of half steps) but have different names are called enharmonic intervals. For example a minor third, an augmented second, and a doubly diminished fourth are enharmonic intervals because they each contain three half steps. You can see the difference in music notation, but you cannot hear the difference.
Intervals larger than an octave are called compound intervals. Compound intervals are always formed from a simple interval with one of the notes raised or lowered an octave. For example a 9th is a second plus an octave and a 10th is a third plus an octave.
| Minor
2nd |
|
Minor 9th |
Major 3rd |
|
Major 10th |
Listening
Click the Familiar Intervals link above to hear these intervals used in familiar tunes.
Other web sites with familiar song intervals
http://www.people.vcu.edu/~bhammel/theory/resources/macgamut_theory/songs_interval_recognize.html
http://en.wikipedia.org/wiki/Ear_training#Interval_recognition
Revised by John Ellinger, Spring 2012.