CS 312 - Week 8.2 Class
CS 312 Audio Programming Winter 2020
Table of Contents
8.2 Class
Harmonic Series
When you press a key on a piano, blow into a wind or brass instrument, pluck a guitar string, or sing you generate a note at a certain frequency. That note is actually composed of several frequencies related by the harmonic series.
Harmonic Series Definition
- Mathematics
A series whose terms are reciprocals of an arithmetic progression \[1{\text{ }} + {\text{ }}\frac{1}{2}{\text{ }} + {\text{ }}\frac{1}{3}{\text{ }} + {\text{ }}\frac{1}{4} \cdots \frac{1}{n}\]
- Music
A series of tones consisting of a fundamental tone and consecutive integer multiples (harmonics) of the fundamental. The fundamental is designated as harmonic 1.
\[{f} + 2{f} + 3{f} + 4{f} \cdots n{f}\]
Alternatively a series of tones consisting of a fundamental tone and and its harmonics whose periods follow the harmonic series.
| Name | Period | Frequency | 100 Hz Fundamental |
| First Harmonic | 1 | f | 100 |
| 2nd Harmonic | 1/2 | 2f | 200 |
| 3rd Harmonic | 1/3 | 3f | 300 |
| 4th Harmonic | 1/4 | 4f | 400 |
| 5th Harmonic | 1/5 | 5f | 500 |
| 6th Harmonic | 1/6 | 6f | 600 |
| 7th Harmonic | 1/7 | 7f | 700 |
| 8th Harmonic | 1/8 | 8f | 800 |
| 9th Harmonic | 1/9 | 9f | 900 |
| 10th Harmonic | 1/10 | 10f | 1000 |
| 11th Harmonic | 1/11 | 11f | 1100 |
| 12th Harmonic | 1/12 | 12f | 1200 |
| 13th Harmonic | 1/13 | 13f | 1300 |
| 14th Harmonic | 1/14 | 14f | 1400 |
| 15th Harmonic | 1/15 | 15f | 1500 |
| 16th Harmonic | 1/16 | 16f | 1600 |
Harmonics, Overtones, And Partials
These terms are often used misused when referring to notes in the harmonic series.
- Harmonics
- Harmonics refer to integer multiples of a fundamental frequency.
Harmonic 1 is the fundamental frequency. - Overtones
- Overtones also refer to integer multiples of a fundamental frequency.
Overtone 1 is harmonic 2. - Partials
- A partial is a non integer multiple of the the fundamental frequency and does not occur in the harmonic series.
Harmonic Series In Musical Notation
The first 16 harmonics of C2 (MIDI 36) are shown below. Harmonics 2f, 4f, 8f, and 16f (the octaves above C2) precisely match the notes on the piano. Because the piano is tuned in equal temperament (hw825) all octaves are in perfectly in tune. All other the notes are slightly out of tune.

Historical tuning systems
Pythagoras is credited with discovering that dividing a string in half produced a tone one octave higher and dividing a string into thirds produced a tone an octave and a fith higher. Medieval and Renaissance musicians used tuning systems where all musical intervals were related by simple fractions 1/2 and 2/3 (octave and fith). Length and frequency are inversely related.
| Length | Frequency | |
|---|---|---|
| Octave lower | x2 | 1/2 |
| Octave higher | 1/2 | x2 |
| Fifth higher | x2/3 | 3/2 |
| Fifth lower | 3/2 | x2/3 |
For example, given string length 1, call it C1, then length C1*2/3 would produce the note a musical fifth higher, G1. A fifth higher than G1 would be length C1*2/3*2/3, D2. If D2 was lowered an octave the length would be D2*2 or D1, the scale note after C1. Using this process the string lengths for all notes of the scale CDEFGABC can be calculated. This scale could then be extended into higher or lower octave by multiplying each note by 1/2 for the octave higher or by 2 for the octave lower, etc.
Musical compositions restricted to this relatively small number of notes produced mathematically pure harmonies that were very pleasing to the ear. However, when composers tried to introduce notes outside of this range like a C# or F# the music sounded harsh or dissonant when certain intervals were used. Experimentation with adjusting the ratios between notes and dividing the octave into 12 parts so that music could be played in different keys eventually led to the system called equal temperament that we use today. The most famous example is Bach's Well Tempered Clavier published in 1722.
Reconciling the tuning problem
We'll use the piano as an example. Start on the lowest C on the piano and continue up for 7 octaves until you reach the highest C on the piano. If you call the lowest frequency f, then the highest frequency is 2^7*f = 128*f.

Now do the same thing tuning by fifths, a 3:2 ratio. After 12 fifths you'll reach the B#7 that lands on the same piano key as C8. If the starting frequency is f, then the ending frequency is (3/2)^12*f = 129.75*f. According to the math B#7 is higher in frequency than C8.

The Comma Of Pythagoras
The difference by which (3/2)^12 exceeds 2^7 is known as the comma of Pythagoras.
\[{\text{ comma of Pythagoras }} = {\text{ }}\frac{{{{\left( {\frac{3}{2}} \right)}^{12}}f}}{{{2^7}f}}{\text{ = }}\frac{{129.75}}{{128}}{\text{ = 1.0136}}\]
Assume f0 is 1Hz. Then
| 12 Fifths | 129.746 |
| 7 Octaves | 128.0 |
| Difference | 1.746 |
| Comma of Pythagoras | 1.0136 |
| B#7 | 4243.12 |
| C8 | 4186.00 |
| Difference | 57.12 |
| B#7/C8 ratio | 1.0136 |
| B#7 * 1/comma | 4186.0 |
Equal Temperament
The Equal Temperament system we use today is one of many tuning systems that have tried to reconcile the pure harmonic series ratios of the Octave (2:1) and the Fifth (3:2). Every octave is contains twelve equal half steps. Every fifth contains seven equal half steps. All octaves remain perfectly in tune. All other notes are calculated using the frequency ratio between half step as done in hw735.
\[{2^{\frac{1}{{12}}}}\]
Equal Temperament in practice
One method of tuning the piano is to tune all octaves perfectly and then flatten each fifth in the cycle of fifths shown above by 1/11 of a comma. That way the cycle of fifths will end on the same frequency as the cycle of octaves. Piano tuners found that the when the interval of a fifth is lowered so that it beats 3 times every 5 seconds, that was the right amount.
On the guitar, every fret is positioned in equal temperament half steps with the 12th fret being the Octave and the 7th fret the fifth. Many guitar players use a method of tuning in harmonics where they play the harmonic on the fifth fret of a lower string and compare it to the harmonic on the seventh fret of the next higher string. If the harmonics match they think it's in tune. Mathematically it's not. The 5th fret harmonic is two octaves above the the open string and the 7th fret harmonic is one octave plus a fifth above the open string. The harmonics produce the pure Pythagorean ratios, the frets produce Equal Temperament ratios. Errors compound themselves when tuning all six strings using harmonics.
String Ensembles and Choral groups are not bound by equal temperament and often use pure ratios in their performances. Violinists and singers trained to produce pure intervals sometimes have trouble adjusting their intonation when accompanied by a piano.
Cents
The audio unit used for measuring small differences in frequency is called a cent. By definition there are 1200 cents in one octave. A half step is 100 cents. This is the general formula to find the cents difference between any two frequencies.
\[{\text{centDifference = 1200 }} \bullet {\text{ lo}}{{\text{g}}_{\text{2}}}\left( {\frac{{f1}}{{f2}}} \right)\]
Trained musicians can detect around a 3 cents difference between two tones.
The Fourier Theorem
Jean Baptiste Joseph Fourier (1768-1830) developed the Fourier Theorem, Fourier Series, and Fourier Transform during his study of heat conduction. Hundreds of books, treatises, college and graduate school mathematics, and engineering courses are devoted to the study of Fourier analysis. The basic premise of Fourier's theorem states that:
Any continuous periodic waveform can be transformed into a sum of sinusoids at integer multiples of the fundamental frequency having well chosen amplitudes and phases.
\[anywave = \sum\limits_{k = 1}^\infty {{A_k}} \sin (k\omega nT + {\theta _k});{\text{ }}\omega = 2\pi {f_0}\]
This formula says that a sawtooth wave, a square wave, a triangle wave, a piano sound, a violin sound, or any periodic sound can be computed by carefully choosing the amplitude and phase values and summing the Fourier series with a fundamental frequency of \({f_0}\).
Fourier Series Harmonics
Given a fundamental frequency \({f_0}\), the Fourier Series consists of sine wave harmonics that are integer multiples of the fundamental frequency. The fundamental frequency is harmonic number one. For example a square wave can be constructed from odd numbered harmonics whose amplitude is the reciprocal of the harmonic number.
\[SquareWave = \frac{4}{\pi }\sum\limits_{n = 1,3,5,7...}^\infty {\frac{1}{n}(\sin (2\pi } n{f_0}))\]
Aliasing
Any frequency in the signal that exceeds the Nyquist Limit (FS/2) will fold back into the output as an unwanted alias frequency. All commercial digital audio software and hardware products aggressively guard against aliasing.
The alias frequency of a square wave exceeding the Nyquist limit is shown in this short code example.
c821_SquareWaveAliasing.cpp
Try this at home.
// calcSquareWaveAliasing.cpp #include <iostream> #include <vector> // Calculate alias frequency if > Nyquist Limit. int main() { const int FS = 44100; const int NYQUIST = FS/2; const int f = 1000; int val; std::vector<float> v; for ( int i = 1; i < 48; ++i ) { val = f*i; if (val <= NYQUIST) std::cout << "f" << i << " = " << val << std::endl; else { val = std::abs( val - FS ); std::cout << "f" << i << " = " << f*i << " aliased to " << val << std::endl; } } }
Output
Note the cycle starts ascends to the Nyquist limit (22050 Hz) then descends to the sampling rate (44100 Hz) and then begins ascending again with a different starting value.
f1 = 1000 f2 = 2000 f3 = 3000 f4 = 4000 f5 = 5000 f6 = 6000 f7 = 7000 f8 = 8000 f9 = 9000 f10 = 10000 f11 = 11000 f12 = 12000 f13 = 13000 f14 = 14000 f15 = 15000 f16 = 16000 f17 = 17000 f18 = 18000 f19 = 19000 f20 = 20000 f21 = 21000 f22 = 22000 f23 = 23000 aliased to 21100 f24 = 24000 aliased to 20100 f25 = 25000 aliased to 19100 f26 = 26000 aliased to 18100 f27 = 27000 aliased to 17100 f28 = 28000 aliased to 16100 f29 = 29000 aliased to 15100 f30 = 30000 aliased to 14100 f31 = 31000 aliased to 13100 f32 = 32000 aliased to 12100 f33 = 33000 aliased to 11100 f34 = 34000 aliased to 10100 f35 = 35000 aliased to 9100 f36 = 36000 aliased to 8100 f37 = 37000 aliased to 7100 f38 = 38000 aliased to 6100 f39 = 39000 aliased to 5100 f40 = 40000 aliased to 4100 f41 = 41000 aliased to 3100 f42 = 42000 aliased to 2100 f43 = 43000 aliased to 1100 f44 = 44000 aliased to 100 // cycle starts ascending again at 900Hz f45 = 45000 aliased to 900 f46 = 46000 aliased to 1900 f47 = 47000 aliased to 2900
We'll demonstrate aliasing effects in hw821_gensquare_phasor using a square wave that has only two values +1.0 and -1.0.
Homework 8.2
hw821_gensquare_phasor
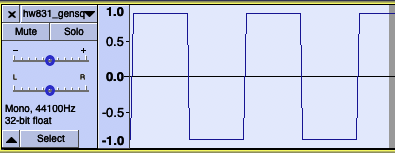
This assignment will construct a 1000Hz square wave using a phasor. As the phasor rotates counterclockwise from 0 to π, the square wave will have a value of +1.0. As it rotates past π to 2π the phasor will have a value of -1.0. When it rotates past 2π you subtract 2π to keep it within the 0 to 2π range.
WARNING:
Turn down the volume before you run the program.
Take off headphones/earbuds.
THIS IS VERY LOUD.
Setup
mkdir $HOME312/cs312/hw82 cd $HOME312/cs312/hw82 mkdir hw821_gensquare_phasor cd hw821_gensquare_phasor touch hw821_gensquare_phasor.cpp touch CMakeLists.txt mkdir build
Open hw821_gensquare_phasor folder in vsCode
hw821_gensquare_phasor.cpp
Copy/paste
#include "sndfile.hh" #include <iostream> #include <vector> #include <cmath> // for M_PI // EITHER typedef float MY_TYPE; #define LIB_SF_FORMAT SF_FORMAT_FLOAT; // SF_FORMAT_MY_TYPE defiend in "sndfile.h" // OR // typedef double MY_TYPE; // #define LIB_SF_FORMAT SF_FORMAT_DOUBLE; // SF_FORMAT_MY_TYPE defiend in "sndfile.h" // END const int FS = 44100; // CD sample rate const MY_TYPE T = 1.0 / FS; // sample period const MY_TYPE k2PI = M_PI * 2.0; const MY_TYPE k2PIT = k2PI * T; std::vector<MY_TYPE> gen_square_phasor(MY_TYPE freq, MY_TYPE ampl, MY_TYPE secs) { std::vector<MY_TYPE> v; MY_TYPE phzNow = 0; MY_TYPE phzIncr = k2PIT * freq; for (int n = 0; n < secs * FS; n++) { /*---------------------------------------------------- Square wave = 1.0 if phznow <= pi Square wave = -1.0 if phzow > pi add sample to v increment phase now wrap around 2pi ----------------------------------------------------*/ } std::cout << "You need to implement gen_square_phasor(...)\n"; return v; } bool samples2wavfile(const char *fname, const std::vector<MY_TYPE> &v) { // code borrowed and modified from libsndfile example sndfilehandle.cc // mostly from create_file(...) and format from main() SndfileHandle file; const int channels = 1; const int srate = FS; const int format = SF_FORMAT_WAV | LIB_SF_FORMAT; file = SndfileHandle(fname, SFM_WRITE, format, channels, srate); // using vector instead of buffer array // C++ vector elements are stored in contiguous memory, same as array // &v[0] is pointer to first element of vector file.write(&v[0], v.size()); return true; } int main(int argc, char *argv[]) { std::vector<MY_TYPE> vsamps = gen_square_phasor(1000.0, 1.0, 1.5); samples2wavfile("hw821_gensquare_phasor_1000Hz.wav", vsamps); return 0; }
CMakeLists.txt
Copy/paste
cmake_minimum_required(VERSION 3.5) set(PROJECT_NAME hw821_gensquare_phasor) project(${PROJECT_NAME}) set(CMAKE_CXX_STANDARD 17) set(CMAKE_CXX_STANDARD_REQUIRED ON) set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -std=c++17 -Wall") # CHANGE THE PATH TO YOUR COMMON FOLDER set(COMMON "/Users/je/cs312/_cs312/common") set(LSF "${COMMON}/libsndfile") set(ULL "/usr/local/lib") add_executable( ${PROJECT_NAME} ${LSF}/sndfile.hh ${PROJECT_NAME}.cpp ) target_include_directories(${PROJECT_NAME} PRIVATE ${COMMON} ${LSF}) target_link_libraries(${PROJECT_NAME} ${ULL}/libsndfile.1.dylib)
Build and run
A hw821_gensquare_phasor_1000Hz.wav will be created in your build folder.
WARNING:
Turn down the volume before you play this file in Audacity.
Take off headphones/earbuds.
THIS IS VERY LOUD.
Play hw821_gensquare_phasor_1000Hz.wav in Audacity.
Plot the spectrum
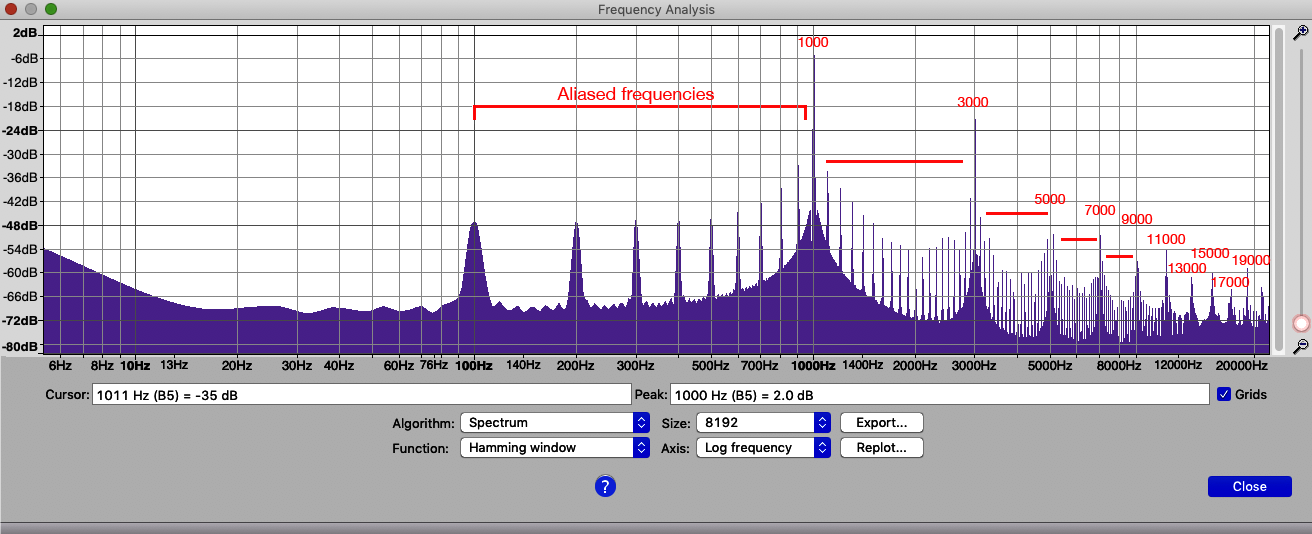
Sharp corners (abrupt slope changes) are produced by high frequencies. Those high frequencies show up in the spectrum.
I had to widen the window to show frequencies up to the Nyquist limit, 22050 Hz. Frequencies higher than the Nyquist limit are aliased to lower frequencies and show up as intermediate peaks between the harmonic peaks. I've drawn red lines indicating where aliased frequencies are present. Aliasing occurs both above and below the fundamental frequency of 1000 Hz.
Ideally we'd like the spectrum to look like this with no intermediate peaks between the harmonic peaks.
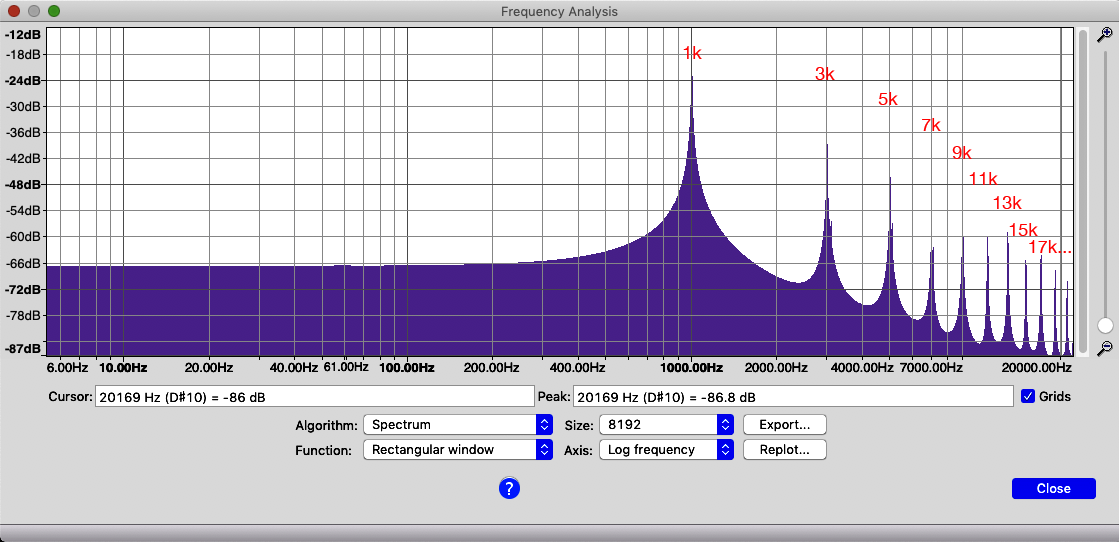
Bandlimited waveforms
A waveform with no frequency content above the Nyquist limit is said to be bandlimited. One method of producing bandlimited waveforms is to use Fourier Series formulas to generate the waveforms and limit the number of harmonics to those below the Nyquist limit.
A 100Hz fundamental could theoretically contain 220 Fourier Series harmonics before exceeding the Nyquist limit. Whether the audible difference in using 50 or 220 harmonics at 100Hz is worth the increased computation time is debatable. Harmonic 50 would equate to 5000 Hz. The highest note on a piano is 4186 Hz. As the fundamental frequency increases past 8000Hz the third harmonic exceeds the Nyquist limit and all waveforms tend to sound like a sine wave. Bandlimited waveforms are the subject of hw822.
hw822_qtplotBLwav
BL is an abbreviation for BandLimited.
The Five Classic Synthesizer Waveforms
The five classic synthesizer waveforms were found on early electronic synthesizers around 1965 and have appeared on synthesizers ever since.
- Sine
- Square
- Sawtooth up (Saw)
- Sawtooth down
- Triangle
The five waveforms can all be generated using the Fourier Series. Bandlimited waveforms can be generating by restricting the number of harmonics allowed based on the fundamental frequency.
In the Fourier Series formulas given below the following terms are used:
- FS is the sampling rate
- T is the sampling period, the inverse of the sampling rate.
- n is an integer harmonic number
- The Greek letter ω (omega) is commonly used to measure frequency in radians per second.
ω = \(2 \pi f\) Hz (cycles per second)
Sine
A pure sine wave has exactly one harmonic, the fundamental frequency. As long as the frequency stays under the Nyquist limit a sine wave is always bandlimited.
\[\sin[n] = \sin (\omega nT + \theta ){\text{; }}\omega = 2\pi {f_0}\]
Equivalent formulas for a sine wave.
\[\sin[n] = sin(\frac{{2\pi n{f_0}}}{{FS}} + \theta ) = sin(2\pi n{f_0}T + \theta ) = sin(\frac{{\omega n}}{{FS}} + \theta ) = sin(\omega nT + \theta )\]
Often the following term is a constant and can be calculated outside of any loops.
\[\frac{{2\pi }}{{FS}} = 2\pi T\]
Saw up
\[\eqalign{ & SawtoothUp[n] = \frac{2}{\pi }\sum\limits_{k = 1}^\infty {\frac{{ - {1^{(k - 1)}}}}{k}\sin (k\omega nT)} {\text{; }}\omega = 2\pi {f_0} \cr & \cr & = \frac{2}{\pi }\left( {\sin (\omega nT) - \frac{1}{2}\sin (2\omega nT) + \frac{1}{3}\sin (3\omega nT) - \frac{1}{4}\sin (4\omega nT) + \frac{1}{5}\sin (5\omega nT)...} \right) \cr} \]
Saw down
\[\eqalign{ & SawtoothDown[n] = \frac{2}{\pi }\sum\limits_{k = 1}^\infty {\frac{1}{k}\sin (k\omega nT)} {\text{; }}\omega = 2\pi {f_0} \cr & \cr & = \frac{2}{\pi }\left( {\sin (\omega nT) + \frac{1}{2}\sin (2\omega nT) + \frac{1}{3}\sin (3\omega nT) + \frac{1}{4}\sin (4\omega nT) + \frac{1}{5}\sin (5\omega nT)...} \right) \cr} \]
Square
\[\eqalign{ & Square[n] = \frac{4}{\pi }\sum\limits_{k = 1}^\infty {\frac{{{1^{(2k - 1)}}}}{{2k - 1}}\sin ((2k - 1)\omega nT)} {\text{; }}\omega = 2\pi {f_0} \cr & \cr & = \frac{4}{\pi }\left( {\sin (\omega nT) + \frac{1}{3}\sin (3\omega nT) + \frac{1}{5}\sin (5\omega nT) + \frac{1}{7}\sin (7\omega nT) + \frac{1}{9}\sin (9\omega nT)...} \right) \cr} \]
Triangle
\[\eqalign{ & Triangle[n] = \frac{8}{{{\pi ^2}}}\sum\limits_{k = 1}^\infty {\frac{{ - {1^{(k + 1)}}}}{{{{(2k - 1)}^2}}}\sin ((2k - 1)\omega nT)} \cr & = \frac{8}{{{\pi ^2}}}\left( {\sin (\omega nT) - \frac{1}{{{3^2}}}\sin (3\omega nT) + \frac{1}{{{5^2}}}\sin (5\omega nT) - \frac{1}{{{7^2}}}\sin (7\omega nT) + \frac{1}{{{9^2}}}\sin (9\omega nT)...} \right) \cr} \]
Setup
Download this zip file
Unzip it. You should see this content.
Copy to your hw82 folder
Copy the hw822_qtplotBLwav folder into your $HOME312/cs312/hw82 folder.
Open the hw822_qtplotBLwav.pro project file in Qt Creator
Change the build folder
Change the Qt build directory to $HOME312/cs312/hw82/hw822_qtplotBLwav/build-debug
Then choose Run qmake from the Build menu.
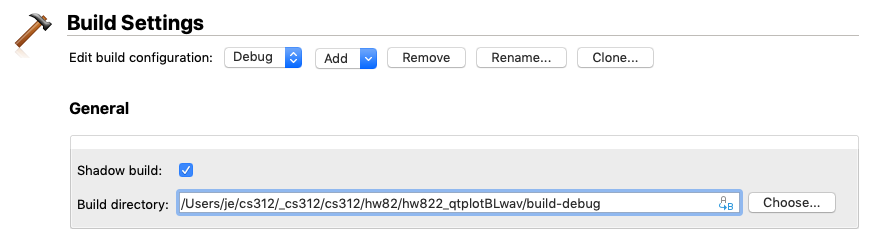
After qmake has finished processing the file you should see this.
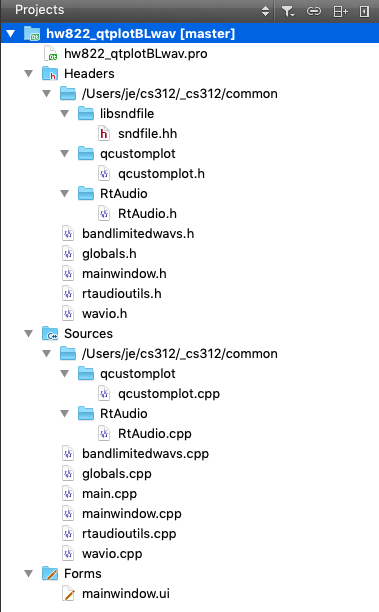
Run the program. You should see this.
The ui-> variable names for the layout widgets are shown below.
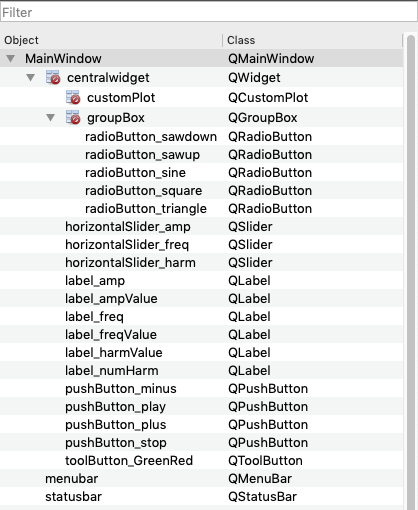
QCustomPlot
The customPlot widget is already setup in the GUI following the same instructions used in hw813_qtwavio_plot.
Sine and Saw Down
I've implemented the Sine and Saw Down waveform functions you. They're in the bandlimitedwavs.h and bandlimitedwavs.cpp files.
Build and run
Select Sine and click the Play button
Move the slider controls.
You should be able to see and hear the Frequency and Amplitude sliders affect the sound.
The number of harmonics slider has no affect because a sine wave has no harmonics.
Select Saw Down
You should be able to see and hear all sliders affect the sound.
If you move the number of harmonics slider to the far left and then slowly move it right you should be able to see and hear the harmonics added to the waveform and the sound one by one.
Select Square
Open the Application tab at the bottom of the Qt Creator window.
You'll immediately see panel fill up with messages.
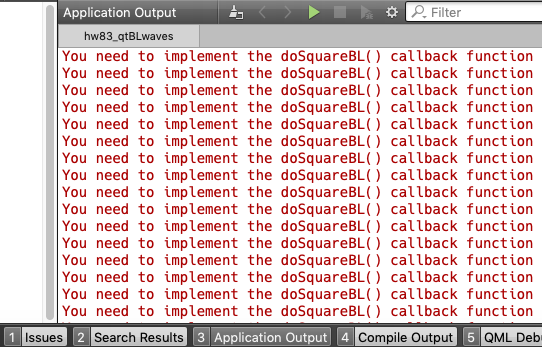
The Square, Saw Up, and Triangle waveforms have been left for you to implement
Assignment 8.2
I've written most of the Qt GUI portion of the hw822_qtBLwaves project for you. You can use my code for the Sine and Saw Down waveforms as an example to implement the other three waveforms. You'll need to use the Saw Up, Square, and Triangle waveforms Fourier Series formulas on the web page.
Three functions are needed for each waveform: a RtAudio callback function, a plotting function, and a calculation function that is called by both the callback and the plotting functions. The highest harmonic number used must remain below the Nyquist frequency. The maximum number of harmonics is limited to 50.
The square, sawUp, and triangle waveforms already produce sound, it's just not the correct sound.
- calcSquareHarmonics()
- doSquareBLCallback()
- doPlotSquareBL()
- calcSawUpHarmonics()
- doSawUpBLCallback()
- doPlotSawUpBL()
- calcTriangleHarmonics()
- doTriangleBLCallback()
- doPlotTriangleBL()
Make use of the Qt Creator debugger
Some of this code is tricky to implement. Setting breakpoints and stepping through your code line by line while examining variables is highly recommended. Think of the Debugger as a programmer's best friend.
My SawDown implementation
I've added comments in the code to help you implement the remaining waveforms.
calcSawDownHarmonics
\[{\text{SawDown}[n] = \frac{2}{\pi }\sum\limits_{k = 1}^\infty {\frac{1}{k}\sin (k\omega nT)} {\text{; }}\omega = 2\pi {f_0} }\]
// This function calculates a single sample that is a sum of integer multiples
// of the fundamental frequency using the Fourier Series formula shown above
// where n is the integer harmonic number and count is the current number of times
// the the doSawDownBLCallback function has been called
// the sin() function always returns values in the range -1.0 to +1.0
MY_TYPE calcSawDownHarmonics( int count )
{
MY_TYPE samp{0};
MY_TYPE sum{0};
std::vector<MY_TYPE> v;
for ( int n = 1; n <= hSlider_numHarmonics; ++n )
{
samp = ( 1.0 / n ) * hSlider_ampl * sin( k2PIT * hSlider_freq * n * count );
v.push_back( samp );
}
// add up all the harmonics and multiply by k2overPI
sum = k2overPI * std::accumulate( v.begin(), v.end(), 0.0 );
return sum;
}
Notes:
k2overPI and k2PIT are const declarations at the top of bandlimitedwavs.cpp.
std::accumulate() is part of the C++ <numeric> library.
Look it up online and you'll discover it can be used in several different ways.
As used above it means "sum all items from v.begin() to v.end() and add 0.0 to the result.
/doSawDownBLCallback( unsigned int nBufferFrames, MY_TYPE* buffer )/
This is called by the RtAudio callback function. It is called repeatedly as long as the RtAudio dac stream is running. It also continuously appends samples to the vsamps vector every time the callback is called.
void doSawDownBLCallback( unsigned int nBufferFrames, MY_TYPE* buffer )
{
// this function is called repeatedly by the rtaudio callback function
// countSawDownCallbacks is declared static so the next time it's called
// it can remember its location for the vsamps vector
static int countSawDownCallbacks = 1;
MY_TYPE sum{0};
// nBufferFrames = kRTABUFFER_SZ = numSamples in callback buffer
unsigned int numSamplesInBuffer = nBufferFrames; // a reminder that for mono files nBufferFrames == numberSamples
for ( unsigned int n = 0; n < numSamplesInBuffer; ++n )
{
// calculate the SawDown Harmonic series for this trip through the callback
sum = calcSawDownHarmonics( countSawDownCallbacks );
// buffer is a pointer address
// *buffer is the value stored at that address
// buffer++ advances the buffer pointer by the size of the objects it contains (MY_TYPE)
*buffer = sum;
buffer++;
*buffer = sum;
buffer++;
// Other C++ functions like vectors better than buffers and pointer arithmetic
vsamps.push_back( sum );
// finished one trip through the callback function
// increment countSawDownCallbacks
countSawDownCallbacks++;
}
}
doPlotSawDownBL()
void doPlotSawDownBL()
{
int count = 0;
MY_TYPE sum{0};
for ( unsigned int n = 0; n < kRTABUFFER_SZ; ++n )
{
sum = calcSawDownHarmonics( count );
plot_buffer[ n ] = sum;
++count;
}
}
Notes:
This function calls the calcSawDownHarmonics() function.
It fills the plot_buffer variable instead of the vsamps vector.
It is not part of the callback function.
It only fills the plot_buffer once.
The plot_buffer variable is declared in globals.h and holds the Y-axis plot data.
The doPlotSawdownBL() function is called in mainwindow.cpp.
void MainWindow::updatePlot( eWaveType e ) { if ( e == esine ) doPlotSine(); else if ( e == esquare ) doPlotSquareBL(); else if ( e == esawup ) doPlotSawUpBL(); else if ( e == esawdown ) doPlotSawDownBL(); else if ( e == etriangle ) doPlotTriangleBL(); plot(); }
Notes:
The updatePlot() function is called whenever the plot needs to be redrawn.
- when the waveform changes
- when the frequency changes
- when the amplitude changes
- when the number of harmonics change
- the updatePlot() function is called in the GUI widget private slots functions.
I used the first code example on this page as a guide to set up the plot.
https://www.qcustomplot.com/index.php/tutorials/basicplotting
Notes for the remaining waveforms
The square and triangle waves use only odd numbered harmonics. This is a common way of testing for odd or even.
for (int i = 1; i< 20; ++i) { odd == 2*i -1; even == 2*i; }
Plot the wave forms
If you implemented the Square, Saw Up, and Triangle waveforms correctly you should see these waveforms using these slider settings:
| Frequency | 500 |
| Amplitude | 0.8 |
| Num Harmonics | 10 |
Sine
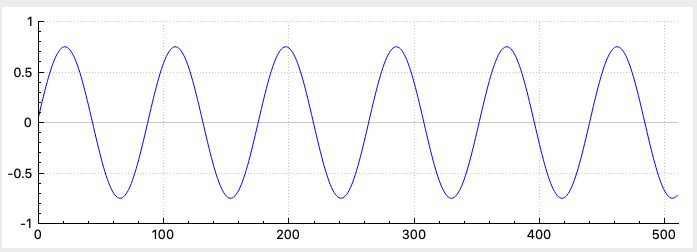
Square
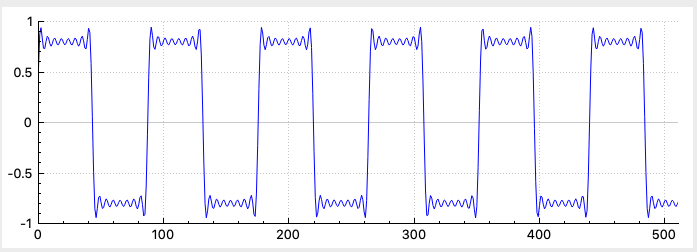
Saw Up
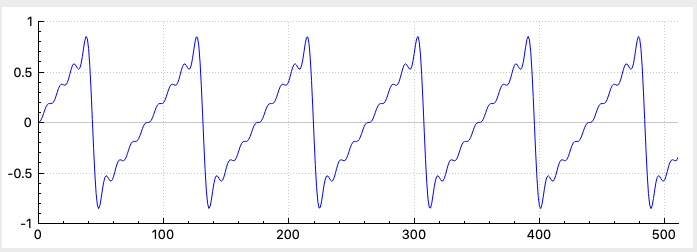
Saw Down
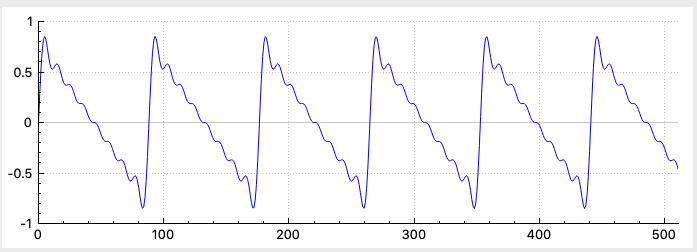
Triangle
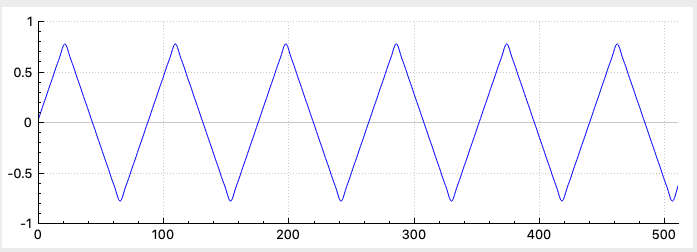
Tasks remaining to implement in mainwindow.cpp
- Square and Triangle waveforms only contain odd numbered harmonics.
Number Harmonics slider should only update the plot and label_value for odd numbers. - Display the amplitude dB value in the amplitude dB label.
- Call setNyquistWarning() when numHarmonics exceeds the Nyquist limit at the current frequency value. The Num Harmonics slider has a fixed range from 1-50 harmonics and has no effect on the sine wave. It does affect the other waveforms. Given a square wave with a fundamental frequency of 1000Hz, harmonic 23 will exceed the Nyquist limit at which point the green square next to the Num harmoncis text label must turn red.
- You need to implement doSave()
Use the wavWrite() code you wrote for hw811_qtwavio
The Save dialog should display the hw82/hw822_qtplotBLwav folder when it opens. You need to implement askSave()
Consult the second example at https://doc.qt.io/qt-5/qmessagebox.html.
Submission
Feel free to email jellinge@carleton.edu on any part of the homework that is unclear to you. Chances are if you have questions other students do too. I will answer those questions by email to everyone in the class. The original sender will remain anonymous. I have tried to provide clues to the homework in the web pages, reading assignments, and labs. Sometimes what seems obvious to me is not obvious to students just learning C++.
Create a folder named hwNN_LastnameFirstname_LastnameFirstname.
Substitute your name and your partner's name for LastnameFirstname_LastnameFirstname.
Remember
- Boilerplate header at top of every file.
- Make sure your program compiles before submitting.
- Programs that compile and produce partially correct output will be graded.
- You can send notes to me in your homework files by enclosing them in block comments.
- Programs that do not compile get an automatic F (59%).
- Submit the homework in only one of the partner's folders.
- Empty your build or build-debug folders using the command emptyBuildFolder.sh
- Only include .h, .cpp, Makefiles, CMakeLists.txt
- Do not include these folders/files
.git
.vscode Double check for the above two folders using this command
ls -a hwNN_LastnameFirstname1_LastnameFirstname2 # if either .git or .vscode exist in the folder you're submitting remove them with # rm -fR .git # rm -fR .vscode
Hand-in folder contents
/common
├── RtAudio
│ ├── RtAudio.cpp
│ └── RtAudio.h
├── RtMidi
│ ├── RtMidi.cpp
│ └── RtMidi.h
├── hw332_CMidiPacket.cpp
├── hw332_CMidiPacket.h
├── hw411_rand_int.cpp
├── hw411_rand_int.h
├── hw421_CDelayMs.cpp
├── hw421_CDelayMs.h
├── hw422_CAppleMidiSynth.cpp
├── hw422_CAppleMidiSynth.h
├── hw423_CMidiTrack.cpp
├── hw423_CMidiTrack.h
├── hw511_CInstrument.cpp
├── hw511_CInstrument.h
├── libsndfile
│ ├── sndfile.h
│ └── sndfile.hh
└── qcustomplot
├── qcustomplot.cpp
└── qcustomplot.h
/hw82
├── hw821_gensquare_phasor
│ ├── CMakeLists.txt
│ ├── build
│ └── hw821_gensquare_phasor.cpp
└── hw822_qtplotBLwav
├── bandlimitedwavs.cpp
├── bandlimitedwavs.h
├── build-debug
├── globals.cpp
├── globals.h
├── hw822_qtplotBLwav.pro
├── main.cpp
├── mainwindow.cpp
├── mainwindow.h
├── mainwindow.ui
├── rtaudioutils.cpp
├── rtaudioutils.h
├── sawdown.wav
├── wavReadWrite.cpp
└── wavReadWrite.h